[BOJ] #2887 행성 터널

백준 2887번 - 행성 터널의 풀이다.

TL;DR

• 밀집 그래프로 보고 Prim으로 풀면 시간 및 메모리 제한에 걸린다.
• 대부분의 간선들은 MST 알고리즘 실행 전에 미리 제거될 수 있다.
  • \(\left| E \right| = \left| V \right|^2\)에서 \(\left| E \right| = 3\left| V \right|\)까지 줄일 수 있다
• 간선을 대부분 제거하여 희소 그래프가 되므로 Kruskal 알고리즘으로 구현한다.

풀이 과정

문제 전문은 BOJ 웹사이트에서 확인할 수 있습니다. (링크)

문제점

처음에는 그래프가 dense하다고 판단하여 Prim 알고리즘으로 풀 생각이었다. 정점의 좌표가 주어지고, 간선의 가중치를 정점 간 거리로 설정하므로 \(\left| E \right|=\left| V \right|^2\)가 되기 때문이다.

하지만 이렇게 풀었더니 메모리와 시간을 초과했다. 간선 가중치를 미리 계산해 저장하려다가 메모리 초과가 발생했고, 가중치를 정점 좌표로부터 실시간으로 계산해서 얻어오도록 변경했으나 시간 초과가 발생했다.

Prim 알고리즘이 밀집 그래프에 적합하다는 사실을 고려해보면, 문제에서 주어진 그래프를 그대로 MST 알고리즘에 적용할 수는 없었다.

간선 제거 - 1차원 공간

간선의 수를 줄여서 sparse graph로 만들 수 있는지 살펴봤다. 이 문제는 각 정점마다 좌표가 주어지고, 가중치가 정점 간 거리로 정의된다는 점에서 정점을 정렬해볼 수 있었다.

문제를 쉽게 생각하기 위해서 3차원 대신 1차원 공간에서의 정점을 생각해봤다.

정점들을 좌표 순서대로 정렬하면, 직관적으로 MST는 이들을 순차적으로 연결한 리스트의 형태임을 알 수 있다.¹ 즉, MST를 구성하는데 필요한 간선은 좌표로 정렬된 상태에서 인접한 정점들 간의 간선만 포함하면 된다. 이와 같이 1차원 공간에서는 MST를 구성하는 간선 \(\left| V \right|-1\)개를 정확히 찾을 수 있다.

간선 제거 - 3차원 공간

3차원 공간에서는 간선들을 일직선상으로 정렬할 수 없기 때문에, 1차원 공간에서처럼 MST를 구성하는 간선을 정확히 특정하기 어렵다. 그러나, 정점이 3차원 좌표를 갖기 때문에 이를 x, y, z 방향 3개의 성분으로 분리하여 각각 정렬해볼 수는 있다.

위 그림에서 정점 b, c는 x축 성분으로 정렬했을 때 서로 인접한다. 정점 a, c는 y, z축 성분으로 각각 정렬했을 때 서로 인접한다. 정점 a, b는 x, y, z축 성분으로 각각 정렬한 3가지 경우 모두에서 서로 인접한다.

이 모형으로부터 아래와 같은 그래프를 그려보겠다.

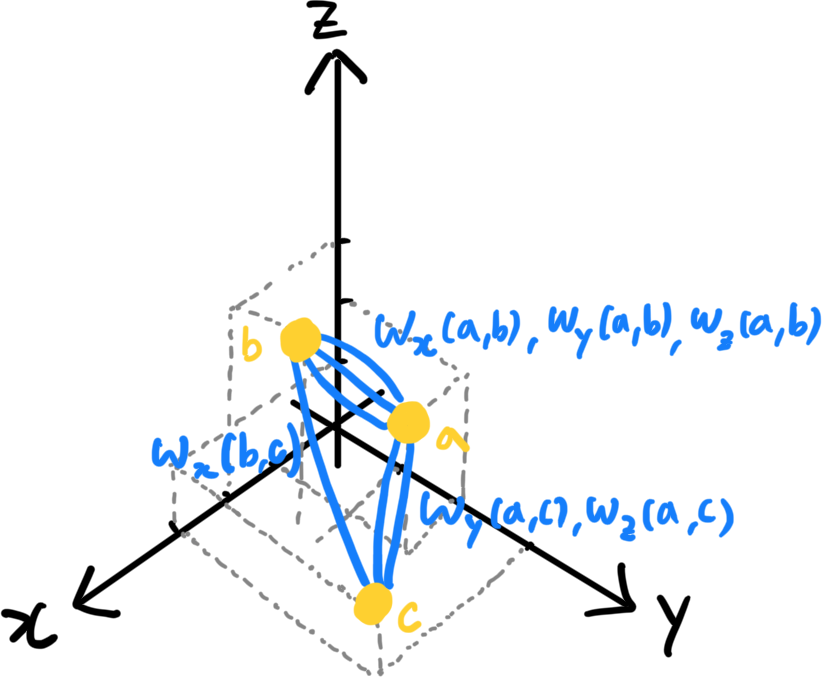
이 그래프는 두 정점 사이에 간선을 여러 개 가질 수 있다. 각 간선의 개수는 두 정점을 특정 성분으로 정렬했을 때 서로 인접하도록 하는 성분의 수와 같고, 가중치는 해당 성분에 대한 두 정점의 좌표 차에 해당한다.

문제에서 주어진 그래프를 살펴보면, 간선의 가중치는 두 정점 간의 거리로 정의된다. 좌표가 각각 \((x, y, z)\)와 \((x', y', z')\)인 두 정점 간의 거리는 \(\min \left( \left| x-x' \right|, \left| y-y' \right|, \left| z-z' \right| \right)\)로 정의한다. 이제 이 간선을 가중치가 각각 \(\left| x-x' \right|\), \(\left| y-y' \right|\), \(\left| z-z' \right|\)인 3개의 간선으로 치환해보자. 이렇게 치환하더라도 MST를 구하는 데는 차이가 없다. 두 정점 사이에 여러 개의 간선이 존재할 경우, MST 알고리즘은 항상 최소 가중치의 간선을 선택하기 때문에 결과적으로 동일한 MST가 만들어진다.

따라서, 우리가 그린 그래프는 문제에서 주어진 그래프의 부분 그래프(subgraph)임을 알 수 있다. 이제, 이 부분 그래프에 포함되지 않은 간선은 MST를 구성할 수 없음을 보이겠다. 어떤 간선 \(vw_x\)가 이 부분 그래프에 추가되지 않았고, 그 양 끝 정점 \(v\), \(w\)의 좌표가 각각 \((x, y, z)\)와 \((x', y', z')\)이며, 가중치는 \(\left| x-x' \right| \gt 0\)이라고 가정하자. 이 간선이 부분 그래프에 추가되지 않은 이유는 어떤 정점 \(u\)가 있어서 그 좌표가 \((x'', y'', z'')\)이고 다음을 만족하기 때문이다.

\[ \begin{align*} \left| x\:-x'' \right| &\geq 0 \\ \left| x'-x'' \right| &\geq 0 \\ \left| x\:-x'\: \right| &= \left| x-x'' \right| + \left| x'-x'' \right| \end{align*} \]

\(\left| x-x'' \right|\)와 \(\left| x'-x'' \right|\)이 각각 \(\left| x-x' \right|\)보다 작기 때문에, Kruskal 알고리즘으로 MST를 찾을 때 가중치가 \(\left| x-x' \right|\)인 간선 \(vw_x\)를 선택하는 시점에는 이미 \(v-u-w\) 간의 경로가 존재하게 되어, 이 간선 \(vw_x\)는 선택될 수 없다.  \(\square\)

앞서 구한 부분 그래프는 간선 개수가 \(\left| E \right|=3\left| V \right|\)로, 기존의 \(\left| E \right|=\left| V \right|^2\)에 비해 간선의 수가 훨씬 적은 희소 그래프(sparse graph)다. Kruskal 알고리즘을 사용하여 제한된 메모리와 시간 내에 MST를 구할 수 있었다.

답안

/**
 * @brief BOJ No. 2887 "행성 터널"
 *
 * @author Minseo Kim <kimminss0@outlook.kr>
 * @details 밀집 그래프로 보고 Prim으로 풀면 시간 및 메모리 제한에 걸린다.
 * 이 문제에서 대부분의 간선들은 MST 알고리즘 실행 전에 미리 제거될 수 있는데,
 * |E| = |V|^2에서 |E| = 3|V|까지 줄일 수 있어 사실상 희소 그래프로 풀 수 있기에
 * Kruskal로 구현한다.
 */

#include <algorithm>
#include <iostream>
#include <tuple>
#include <utility>
#include <vector>

using namespace std;

class UnionFind {
private:
  vector<int> parent;

public:
  UnionFind(int N) : parent(N) {
    for (int i = 0; i < N; i++) {
      parent[i] = i;
    }
  }

  int find(int x) {
    if (parent[x] == x) {
      return x;
    }
    // path compression
    return parent[x] = find(parent[x]);
  }

  bool unite(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX == rootY) {
      return false;
    }
    parent[rootX] = rootY;
    return true;
  }
};

int main(void) {
  cin.tie(nullptr)->sync_with_stdio(false);

  int N;
  cin >> N;

  // idx, coordinate (along the axis)
  vector<pair<int, int>> x(N), y(N), z(N);

  for (int i = 0; i < N; i++) {
    x[i].first = i;
    y[i].first = i;
    z[i].first = i;
    cin >> x[i].second >> y[i].second >> z[i].second;
  }

  if (N == 1) {
    cout << 0;
    return 0;
  }

  // sort by coordinate
  auto cmp = [](pair<int, int> a, pair<int, int> b) -> bool {
    return a.second < b.second;
  };
  sort(x.begin(), x.end(), cmp);
  sort(y.begin(), y.end(), cmp);
  sort(z.begin(), z.end(), cmp);

  // w, v, u
  vector<tuple<int, int, int>> edges;
  edges.reserve(N * 3);
  for (const auto &ax : {x, y, z}) {
    for (int it1 = 0, it2 = 1; it2 < N; it1++, it2++) {
      int v = ax[it1].first;
      int u = ax[it2].first;
      int w = abs(ax[it1].second - ax[it2].second);
      edges.emplace_back(make_tuple(w, v, u));
    }
  }
  // sort by weight, ascending
  std::sort(edges.begin(), edges.end(),
            [](auto a, auto b) -> bool { return get<0>(a) < get<0>(b); });

  // KruskalMST
  UnionFind uf(N);
  int mstWeight = 0;
  for (auto [w, v, u] : edges) {
    if (uf.unite(v, u)) {
      mstWeight += w;
    }
  }
  cout << mstWeight;

  return 0;
}